5-3. 変動係数を求めてみよう
【夕方は走って登ってジャンプ】夕方、日が落ちて涼しくなってくると猫たちにとってのゴールデンタイムが始まります。空き地で追いかけっこ、木登り、虫取り。
次の表は、空き地にある猫たちが大好きな木の高さをまとめたものです。
| 枝が立派な木(m) | 赤い実がなる木(m) | 大きな葉っぱの木(m) |
|---|---|---|
| 12 | 4 | 0.8 |
| 15 | 5 | 1.2 |
| 15 | 3 | 1.0 |
| 12 | 5 | 1.6 |
| 13 | ― | 0.7 |
| 14 | ― | ― |
まず、平均値と標準偏差を求めます。
| 枝が立派な木(m) | 赤い実がなる木(m) | 大きな葉っぱの木(m) | |
|---|---|---|---|
| 平均 | 13.5 | 4.3 | 1.1 |
| 標準偏差 | 1.4 | 1.0 | 0.4 |
この表を見ると、高さのばらつきが一番大きいのは「枝が立派な木」であることが分かります。ただし、3種類の木の高さの平均値が大きく異なることから、平均値に対する標準偏差の大きさを比較するほうが良い場合があります。
この、平均値に対するデータとばらつきの関係を相対的に評価するための値のことを「変動係数」といいます。変動係数は次の式から求められます。
変動係数=標準偏差÷平均値
この式を使って、それぞれの木の変動係数を求めてみます。
枝が立派な木の変動係数=1.4÷13.5=0.1
赤い実がなる木=1.0÷4.3=0.2
大きな葉っぱの木=0.4÷1.1=0.3
この結果をまとめると次のようになります。
| 枝が立派な木(m) | 赤い実がなる木(m) | 大きな葉っぱの木(m) | |
|---|---|---|---|
| 平均 | 13.5 | 4.3 | 1.1 |
| 標準偏差 | 1.4 | 1.0 | 0.4 |
| 変動係数 | 0.1 | 0.2 | 0.3 |
変動係数を計算すると、平均値に対しては大きな葉っぱの木の高さが最も相対的にばらつきが大きいという結果になりました。
'지식 > 경제수학' 카테고리의 다른 글
| 라스파이레스지수(기준년 수량고정), 파셔지수(비교년 수량고정) (0) | 2018.09.17 |
|---|---|
| 箱ひげ図を描いてみよう (0) | 2018.09.17 |
| 사분위수 (0) | 2018.09.17 |
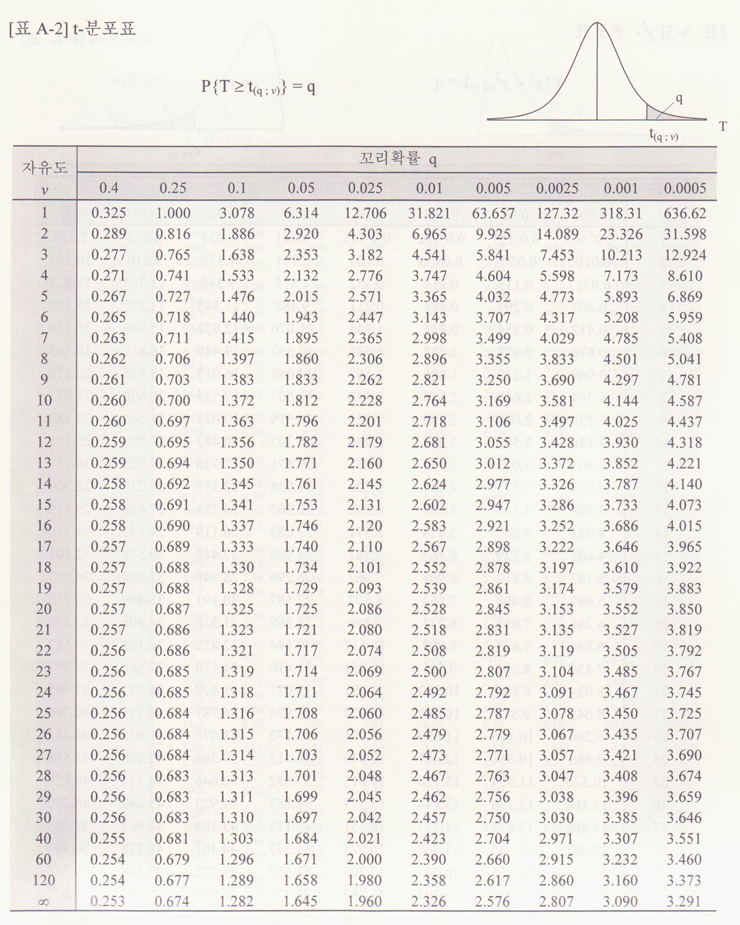
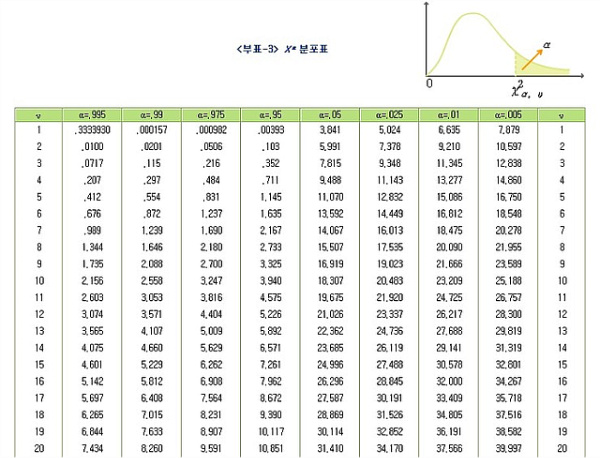
| [경제통계]z분포, 카이제곱분포, t분포, 카이제곱분포표 보는법, t분포표 보는법 (0) | 2017.12.19 |
| [경제통계]정규분포(normal distribution), 정규분포의 평균도출, 표준정규분포, 표준화 (1) | 2017.12.19 |