1. 푸아송 분포 (poisson distribution)
ⅰ. 푸아송분포의 언어적 의미
이산확률분포의 하나로 독립적인 각각의 사건이 발생하는 상한이 정해지지 않은 경우의 확률 분포.
예를 들어,
1년 동안 여기에 사람이 몇 명이나 올까?
1시간 동안 생산라인을 돌리면 불량품이 몇 개 나올까?
오늘의 출생률은?
이 교차로에서 오늘 사고가 날 확률은?
1제곱킬로미터의 영역 내에 특정 종류의 식물이 몇개나 발견될까?
처럼, 각각의 사건은 독립적이지만 발생의 상한이 정해지지 않은 확률분포를 의미한다.
ⅱ.푸아송분포의 확률분포
구간 내의 평균 발생 횟수를 람다λ 라고 하면,
![]()
이때 푸아송 분포는 이산확률분포이기 때문에 P(x)에 대하여 확률 표현이 가능하다. (무슨 말이냐하면, 이산확률분포가 아닌 연속확률분포에서는 P(x) = 0 이라는 것을 말하고 싶은 것)
ⅲ. 푸아송 분포의 분포함수(푸아송분포의 확률질량함수)
![]()
ⅳ. 푸아송함수의 E(x), V(x) 도출
①E(x)

②V(x) = E(x^2) - {E(x)}^2

ⅴ. 푸아송 분포의 예제
어느 교차로에는 한달 (30일) 평균 30건의 사고가 발생한다고 할 때, 다음의 물음에 답하여라
①한달에 20건의 사고가 발생할 확률
한달 평균 30건의 사고가 발생하므로 λ = 30이라고 둘 수 있다.
![]()
②하루에 2건 이상의 사고가 발생할 확률
하루평균 1건의 상고가 발생하므로 λ = 1이라고 둘 수 있다.
![]()
※예제에서 볼 수 있는 바와 같이, 문제에서 제시된 단위를 풀이에 필요한 λ의 단위로 환산하는 것에 주의한다.
그림1. λ = 30일때 푸아송분포의 확률질량함수
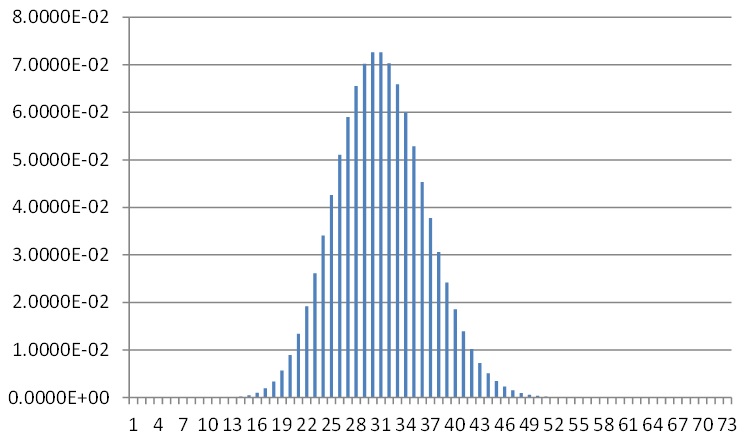
2. 베르누이분포(Bernoulli Distribution)
변수가 2종류 (성공 or 실패) 밖에 존재하지 않는 실험에서 사용하는 분포. 예를 들면, 동전을 단한번 던지는 실험에서 앞면에 나오면 1, 뒷면이 나오면 0 이라고 할때 이는 베르누이의 분포에 해당한다.
ⅰ. 베르누이 분포의 확률질량함수

ⅱ. 베르누의 분포의 평균과 분산
평균 : p
분산 : pq
3. 이항분포
각 시행이 독립적인 베르누이 시행이 n회 반복해서 시행된 것.
(이항분포는 고등학교에서도 다루는 내용이므로 이하내용생략)
'지식 > 경제수학' 카테고리의 다른 글
| [경제통계]지수분포 (0) | 2017.12.19 |
|---|---|
| [경제통계]균등분포 (0) | 2017.12.19 |
| [경제통계]헷갈리는 통계 기본 용어 사전 (0) | 2017.12.19 |
| [수학논리]귀류법, 귀류법의 예, 귀류법은 항상 옳은가? (0) | 2017.12.19 |
| [경제통계]베이즈 정리, 베이즈정리의 예 (0) | 2017.12.19 |