헷갈리는 통계 기본 용어 사전
*변수 : 하나하나의 사건을 나타내는 말. 예를 들어, 주사위에 6개의 사건 1,2,3,4,5,6 이 있을 때 1~6은 각 하나의 변수이다.
*도수 : 사건이 거듭하는 횟수. 주사위를 3번 던져서 1이 두번 나올 때 1이나온 사건의 도수는 2이다.
*도수분포 : 각 변수가 등장한 횟수만큼의 도수를 표로 나타낸 것.
*확률변수 : 표본공간 내에서 변수 X가 취할 수 있는 각 값에 확률이 정해져 있을때 변수 X를 확률이 딸려있는 변수라하여 확률변수라고 부른다. 가령 주사위에서 변수 x=1은 확률변수 X이자 그 확률은 1/6이다.
*이산확률변수 : 확률변수 X는 X가 서로 떨어져 있는 값을 취하는 변수일때 이를 이산확률변수 라고 한다. 가령, 주사위의 눈같은 경우 각 확률변수 1,2,3,4,5,6은 서로 떨어져 구분된다.
*연속확률변수 : 확률변수 X가 서로 연속적으로 어떤 구간안에 있을 경우 그 변수들을 연속확률변수라고 한다. 가령, 시간, 키, 온도 등이 예로 들어질 수 있다.
*확률분포 : 확률변수 X가 취하는 변수xi와 X가 취하는 확률 pi의 대응 관계를 나타낸 것을 확률 분포라고 한다. 예를 들어, 주사위를 던질때 1의 확률은 1/6, 2의 확률은 1/6 . . . 6의 확률은 1/6 일때 각 변수와 확률관의 관계를 분포표위에 나타낸 것을 의미한다.
*이산확률분포 : 확률변수 x가 이산변수 일때의 분포. 베르누이분포, 이항분포, 다항분포, 푸아송분포 등이 이에 해당.
*연속확률분포 : 확률변수x가 연속변수 일때의 분포. 균일분포, 정규분포, 표준정규분포, 지수분포, 감마분포등이 이에 해당
*확률분포함수 : 어떤 사건이 존재할 때 각 변수의 확률분포에 의해서 만들어지는 분포전체의 모양을 확률함수 라고 한다.
*확률질량함수 : 이산확률변수에 의한 확률분포 함수.
*확률밀도함수 : 연속확률변수에 의한 확률분포 함수. x축과 확률밀도함수 사이의 넓이의 합은 1이며, 각 구간은 구간의 확률을 나타낸다.
| TIP | 확률분포와 확률분포함수의 개념 구분 | ||||||||||
확률분포와 확률분포함수의 개념이 특히나 헷갈릴 수 있으므로 보충하여 설명하기로 한다. 결론부터 말하면, 확률분포와 확률분포함수는 변수가 이산이냐 연속이냐에 의해 총 네가지로 구분된다.
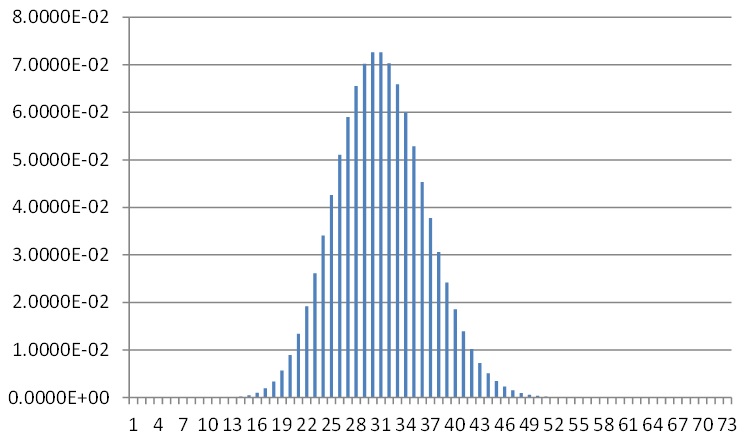
아래의 푸아송 분포의 확률질량함수와 정규분포의 확률밀도함수를의 그래프를 통해 위 네가지를 구분해보자. 그림1. λ = 30일때 푸아송분포의 확률질량함수
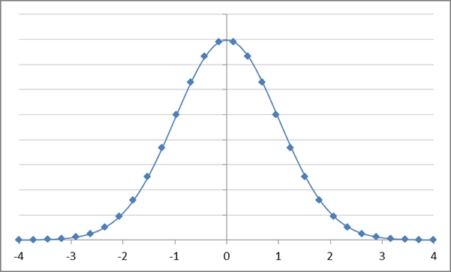
①변수 X가 이산확률변수 일 때, 이산확률분포는 P(X)로 표현되며, 그림1에서 하나하나의 변수에 따른 각각의 파란 막대를 의미하는 개념이다. 확률질량함수는 F(X),f(X)로 표현되며, 모든 확률분포가 더해져 만들어진 전체를 나타내는 개념으로 ∑P(X)이다. 그림2. 어떤 사건의 확률밀도함수(정규분포)
②변수 X가 연속확률변수 일 때, 연속확률분포는 P(X)로는 표현될 수없다. 왜냐하면 각 변수가 이산이 아닌 연속이기 때문에 P(X)=0이기 때문이다. 대신 연속확률분포는 구간으로 표현이 가능한데 확률밀도함수는 F(X),f(X)로 표현되며, 확률밀도함수를 적분하여 연속확률분포를 표현한다. | |||||||||||
*균등분포(일양분포) : 연속확률분포 중 구간내의 값들이 나타날 가능성이 균등한 분포. 확률밀도함수가 사각형의 모양을 띈다.
'지식 > 경제수학' 카테고리의 다른 글
| [경제통계]균등분포 (0) | 2017.12.19 |
|---|---|
| [경제통계]이산확률분포 - 푸아송분포,평균분산도출,푸아송분포의예제, 베르누이분포, 이항분포 (0) | 2017.12.19 |
| [수학논리]귀류법, 귀류법의 예, 귀류법은 항상 옳은가? (0) | 2017.12.19 |
| [경제통계]베이즈 정리, 베이즈정리의 예 (0) | 2017.12.19 |
| [경제통계]도수분포표, 히스토그램, 로렌츠곡선, 지니계수 (0) | 2017.12.19 |