편상관계수

26-4. 偏相関係数

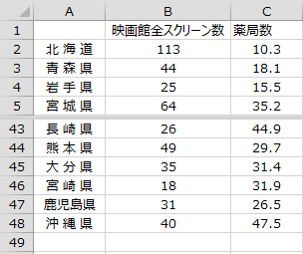
次のデータは2015年12月末時点の各都道府県内にある映画館のスクリーンの合計数と可住地面積100当たりの薬局数を表したものです。このデータを用いて相関係数を算出すると、「0.82」でした。つまり、映画館のスクリーン数と薬局の数には強い相関があるという結果でした。

出典：総務省統計局 社会生活統計指標－都道府県の指標－2015

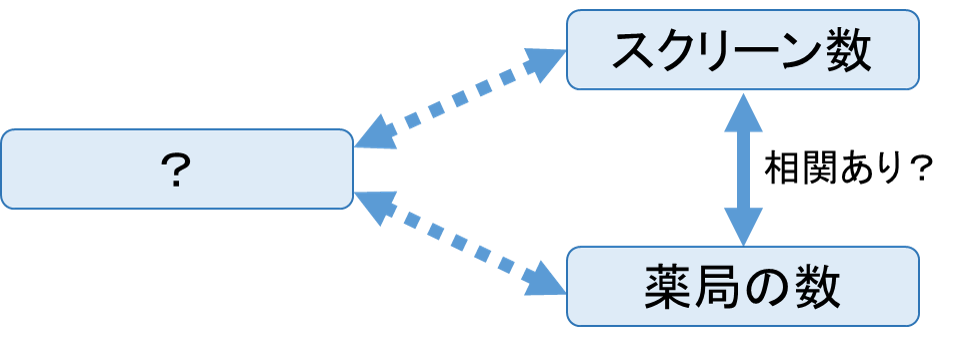
しかし、一般的に考えて都道府県ごとの映画館のスクリーン数と可住地面積100当たりの薬局の数は直接的に関係がないような気がします。映画館のスクリーン数が多いから薬局の出店数が増えるわけでも、薬局の数が多いから映画館のスクリーン数が増えるわけでもないためです。このような場合には、「第3の因子」の存在を考慮する必要があります。

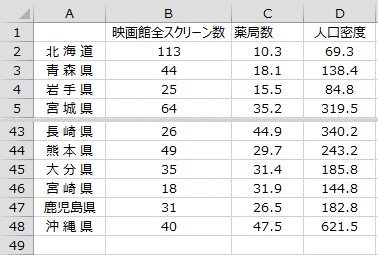
上のデータに各都道府県の人口密度のデータを加えてみます。

出典：総務省統計局 社会生活統計指標－都道府県の指標－2015

人口密度と映画館のスクリーン数、及び人口密度と薬局の数の相関係数はそれぞれ「0.85」と「0.98」でした。つまり、人口密度がスクリーン数と薬局の数それぞれと強い相関を持っているため、これらの影響を除いた上で映画館のスクリーン数と薬局の数との相関関係を調べる必要があります。

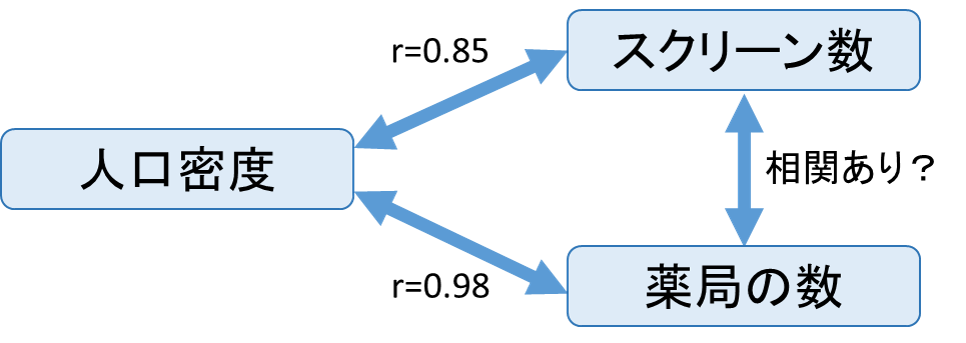
映画館のスクリーン数と薬局の数のような相関関係のことを「見かけ上の相関」や「疑似相関」といいます。見かけ上の相関がある場合は、相関係数ではなく第3の因子の影響を除いた相関係数である「偏相関係数」を用いて相関関係を評価します。1つ目の因子をx、2つ目の因子をy、3つ目の因子をzとおき、xとyの相関係数を、yとzの相関係数を、zとxの相関係数をとします。これらを用いると、zの影響を除いたxとyの偏相関係数を次の式から求められます。

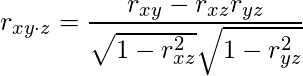
上のデータの映画館のスクリーン数、薬局の数、人口密度をそれぞれx、y、zとおくと、相関係数はそれぞれ、、となるので、偏相関係数は「-0.13」となります。

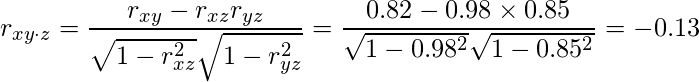
この結果から、映画館のスクリーン数と薬局の数との相関は、実はあまり強くないことが分かります。