9-3. logistic regression cost function

$$\theta^{T}X = w_{0}x_1^m+w_{1}x_2^m+...+w_{n}x_n^m)$$

 

・y의 값에 따라, 비용함수가 바뀐다.

 

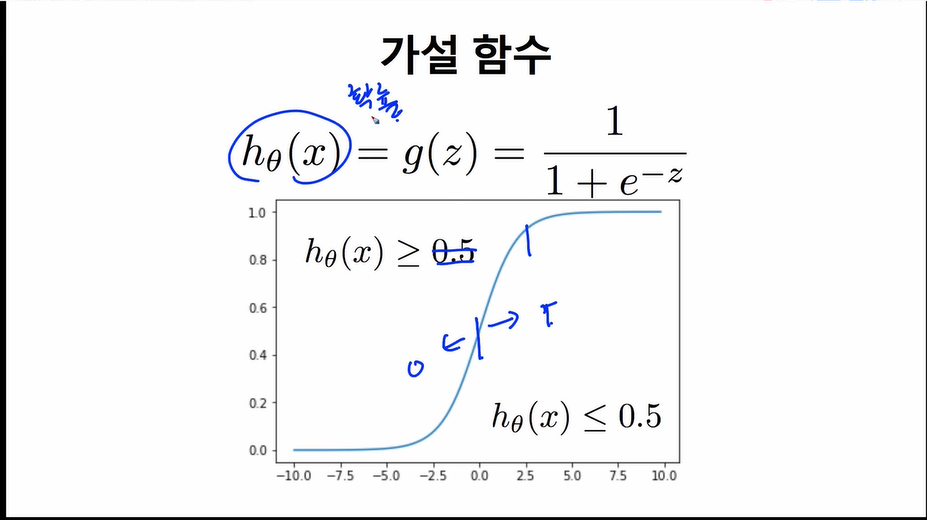
・위위의 스크린 샷에서, y의 값에 따라 비용함수가 바뀌므로, 위와같은 식으로 비용함수가 정의된다.

$$y^{(i)}\log_{}{h_{\theta}}(x^{(i)})+(1-y^{(i)})\log_{}{(1-h_{\theta}(x^{(i)})})$$
$$에서$$
$$y=1이면, (1-y^{(i)})\log_{}{(1-h_{\theta}(x^{(i)})})=0이되고$$ 
$$y=0이면, y^{(i)}\log_{}{h_{\theta}}(x^{(i)})이 0이됨$$

 

$$이때 \theta x^{i}는 \theta^{T}X = w_{0}x_{0}+w_{1}x_{1}+w_{3}x_{3}+...에 주의$$