[Python] 어떤 스케일러를 쓸 것인가?(https://mkjjo.github.io/python/2019/01/10/scaler.html)
By MK on January 10, 2019
데이터를 모델링하기 전에는 반드시 스케일링 과정을 거쳐야 한다. 스케일링을 통해 다차원의 값들을 비교 분석하기 쉽게 만들어주며, 자료의 오버플로우(overflow)나 언더플로우(underflow)를 방지하고, 독립 변수의 공분산 행렬의 조건수(condition number)를 감소시켜 최적화 과정에서의 안정성 및 수렴 속도를 향상 시킨다.
특히 k-means 등 거리 기반의 모델에서는 스케일링이 매우 중요하다.
회귀분석시 조건수라는 개념이 있는데 그 내용은 아래와 같다.
회귀분석에서의 조건수
고유값(Eigenvalue)과 관련된 조건수(Condition Number)의 관계를 나타내는 산식은 c = condeig(A)이다.
A의 고유값에 대한 조건수의 벡터를 반환한다. 이 조건수는 좌고유벡터와 우고유벡터 사이 각도의 코사인의 역수이다..라고 하는데,
복잡한 얘기는 생략하고 핵심만 파악해보자.
함수의 조건수(condition number)는 argument에서의 작은 변화의 비율에 대해 함수가 얼마나 변화할 수 있는지 에 대한 argument measure이다.
조건수가 크면 약간의 오차만 있어도 해가 전혀 다른 값을 가진다. 따라서 조건수가 크면 회귀분석을 사용한 예측값도 오차가 커지게 된다.
회귀분석에서 조건수가 커지는 경우는 크게 두 가지가 있다.
1) 변수들의 단위 차이로 인해 숫자의 스케일이 크게 달라지는 경우. 이 경우에는 스케일링(scaling)으로 해결한다.
2) 다중 공선성 즉, 상관관계가 큰 독립 변수들이 있는 경우, 이 경우에는 변수 선택이나 PCA를 사용한 차원 축소 등으로 해결한다.
그리고 다음과 같은 경우에는 로그 함수 혹은 제곱근 함수 등을 사용하여 변환된 변수를 사용하면 회귀 성능이 향상될 수도 있다.
독립 변수나 종속 변수가 심하게 한쪽으로 치우친 분포를 보이는 경우 독립 변수와 종속 변수간의 관계가 곱셈 혹은 나눗셉으로 연결된 경우 종속 변수와 예측치가 비선형 관계를 보이는 경우
대부분 우리가 다루는 데이터 중 금액처럼 큰 수치 데이터에 로그를 취하게 되는 이유 이기도 하다.
보통 이런 데이터는 선별적으로 로그를 취한 후 모델링 전 전반적으로 스케일링을 적용한다.(in my opinion)
그렇다면 어떤 스케일링 기법을 적용해야할까?
스케일링의 종류
Scikit-Learn에서는 다양한 종류의 스케일러를 제공하고 있다. 그중 대표적인 기법들이다.
데이터를 기준으로 범위를 변환하는 법 : 4가지 (https://data-newbie.tistory.com/23)
|
변환법
|
설명 |
|
StandardScaler |
평균 0 분산 1로 변경 모든 특성이 같은 크기 가지게 한다 -> 최솟값과 최댓값 크기를 제한하지는 않는다. |
|
RobustScaler |
특성들이 같은 스케일을 갖게 된다는 것은(Standscaler 와 비슷) -> 하지만 평균과 분산 대신 중간 값(median) 와 사분위값(quantile) 사용한다 -> 측정 에러의 영향을 받지 않는다 (이상치 영향 안받음) |
|
MinMaxScaler |
모든 특성이 정확하게 0과 1 사이에 위치하도록 한다 2차원 데이터 셋의 경우에는 x 축의 0과 1 , y축 0과 1 |
|
Normalizer |
특성 벡터의 유클리드안 길이가 1이 되도록 데이터 포인트를 조정한다. -> 다른 말로하면 지름이 1인 원에(3차원에서는 구)에 데이터 포인트를 투영합니다. -> 이 말은 데이터 포인트가 다른 비율로(길이에 비례) 스케일이 조정된다는 것이다 -> 이러한 정규화는 특성 벡터의 길이는 상관없고 데이터 방향(도는 각도)만이 중요할 때 많이 사용 된다. |
1. StandardScaler
평균을 제거하고 데이터를 단위 분산으로 조정한다. 그러나 이상치가 있다면 평균과 표준편차에 영향을 미쳐 변환된 데이터의 확산은 매우 달라지게 된다.
따라서 이상치가 있는 경우 균형 잡힌 척도를 보장할 수 없다.
from sklearn.preprocessing import StandardScaler standardScaler = StandardScaler() print(standardScaler.fit(train_data)) train_data_standardScaled = standardScaler.transform(train_data)
2. MinMaxScaler
모든 feature 값이 0~1사이에 있도록 데이터를 재조정한다. 다만 이상치가 있는 경우 변환된 값이 매우 좁은 범위로 압축될 수 있다.
즉, MinMaxScaler 역시 아웃라이어의 존재에 매우 민감하다.
from sklearn.preprocessing import MinMaxScaler minMaxScaler = MinMaxScaler() print(minMaxScaler.fit(train_data)) train_data_minMaxScaled = minMaxScaler.transform(train_data)
3. MaxAbsScaler
절대값이 0~1사이에 매핑되도록 한다. 즉 -1~1 사이로 재조정한다. 양수 데이터로만 구성된 특징 데이터셋에서는 MinMaxScaler와 유사하게 동작하며, 큰 이상치에 민감할 수 있다.
from sklearn.preprocessing import MaxAbsScaler maxAbsScaler = MaxAbsScaler() print(maxAbsScaler.fit(train_data)) train_data_maxAbsScaled = maxAbsScaler.transform(train_data)
4. RobustScaler
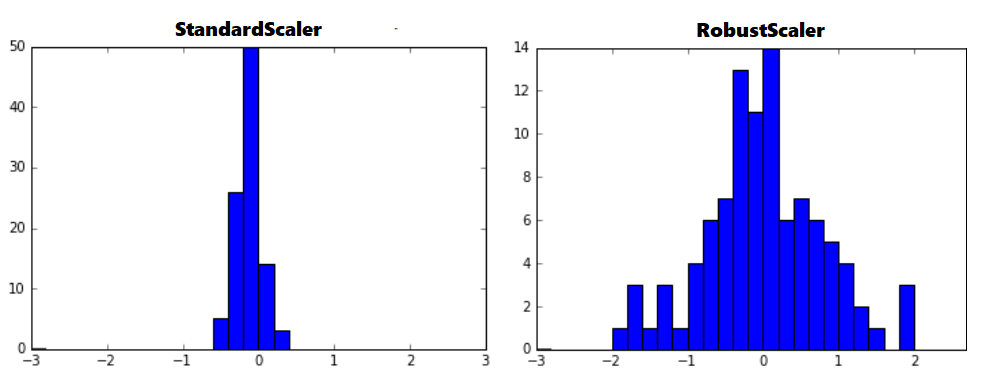
아웃라이어의 영향을 최소화한 기법이다. 중앙값(median)과 IQR(interquartile range)을 사용하기 때문에 StandardScaler와 비교해보면 표준화 후 동일한 값을 더 넓게 분포 시키고 있음을 확인 할 수 있다.
IQR = Q3 - Q1 : 즉, 25퍼센타일과 75퍼센타일의 값들을 다룬다.
아웃라이어를 포함하는 데이터의 표준화 결과는 아래와 같다.
from sklearn.preprocessing import RobustScaler robustScaler = RobustScaler() print(robustScaler.fit(train_data)) train_data_robustScaled = robustScaler.transform(train_data)
결론적으로 모든 스케일러 처리 전에는 아웃라이어 제거가 선행되어야 한다. 또한 데이터의 분포 특징에 따라 적절한 스케일러를 적용해주는 것이 좋다.
데이터 분포별 변환 결과
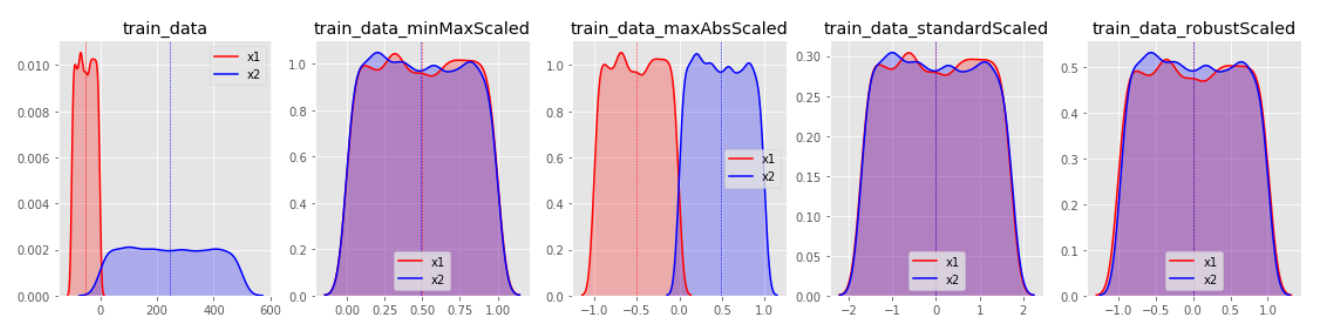
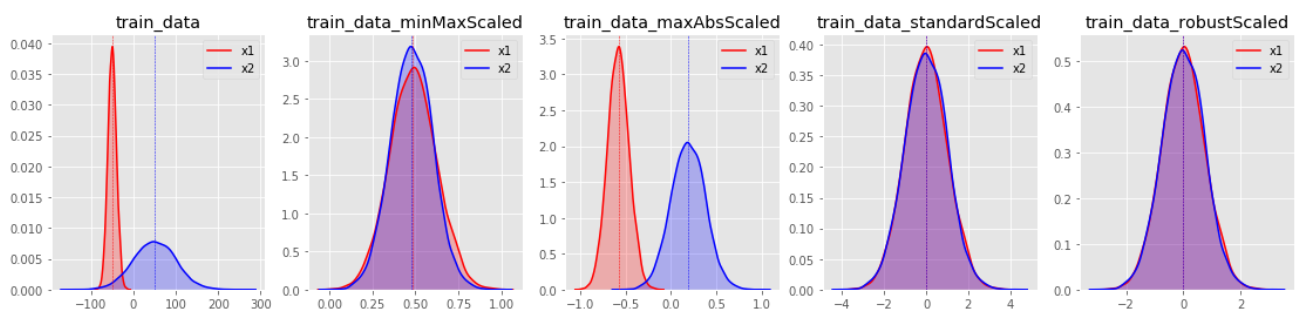



변환 분포를 살펴보면 StandardScaler와 RobustScaler의 변환된 결과가 대부분 표준화된 유사 형태의 데이터 분포로 반환된다.
MinMaxScaler특정값에 집중되어 있는 데이터가 그렇지 않은 데이터 분포보다 1표준편차에 의한 스케일 변화값이 커지게 된다. 한쪽으로 쏠림 현상이 있는 데이터 분포는 형태가 거의 유지된채 범위값이 조절되는 결과를 보인다.
MaxAbsScaler의 경우, MinMaxScaler와 유사하나 음수와 양수값에 따른 대칭 분포를 유지하게 되는 특징이 있다.
그리고 마지막 이미지를 통해 살펴보면, 대부분의 스케일링 기법에서 아웃라이어는 변환 효과를 저해하는 요소임이 드러난다.
유의해야할 점은, 스케일링시 Feature별로 크기를 유사하게 만드는 것은 중요하지만, 그렇다고 모든 Feature의 분포를 동일하게 만들 필요는 없다.
특성에 따라 어떤 항목은 원본데이터의 분포를 유지하는 것이 유의할 수 있다. 예로 데이터가 거의 한 곳에 집중되어 있는 Feature를 표준화시켜 분포를 같게 만들었을때 작은 단위의 변화가 큰 차이를 나타내는 것으로 반영될 수 있기 때문이다.
'C Lang > machine learing' 카테고리의 다른 글
| 8-6. polynomial regression (0) | 2019.05.06 |
|---|---|
| 8-5. sklearn Linear Model family (0) | 2019.05.06 |
| 8-4. Regularization – L1, L2 (0) | 2019.04.20 |
| 8-3. Overfitting and regularization overview (0) | 2019.04.18 |
| 8-2. SGD implementation issues(convergence process, time-consuming, multivariate, learning rate decay, terminal condition setup) (0) | 2019.04.16 |