







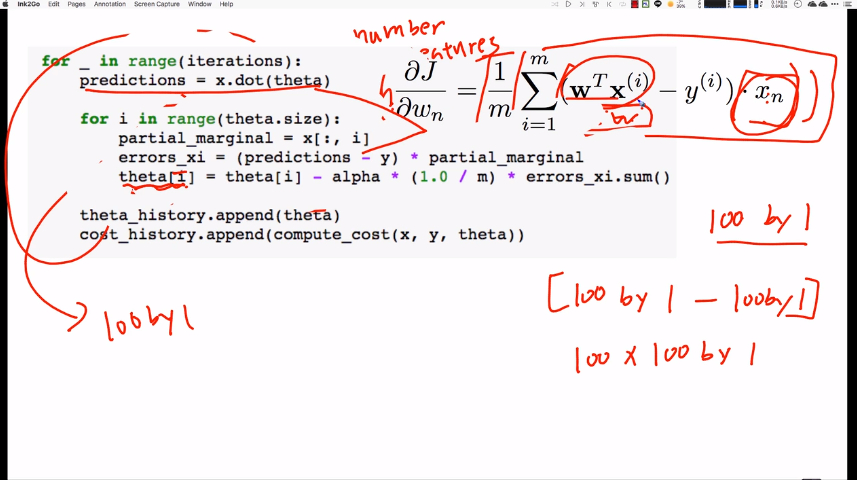
각 파라미터의 메트릭스, 벡터의 shape를 팔로우 하는 것이 이해에 중요하다.
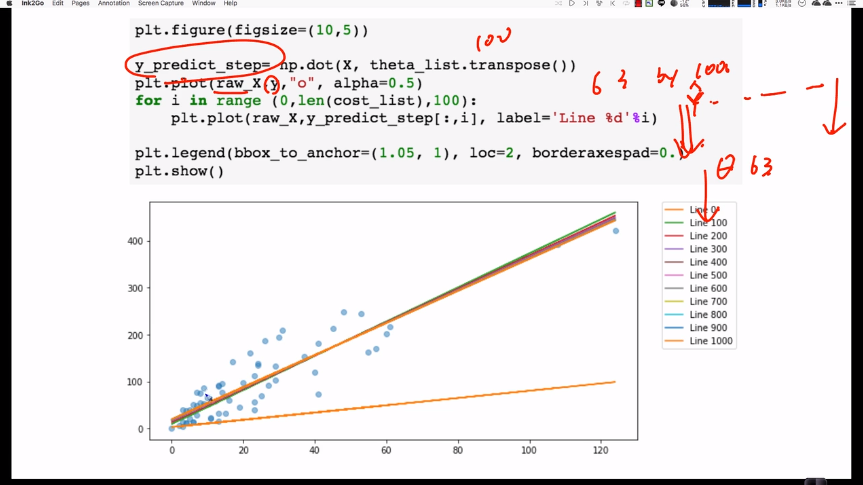
raw_X가 (63,)데이타라고 할 때,
# [X] (63,2) matrix
# [Y] (63,) vector
# [w] (2,)vector
# [alpha] scalar
# [m] 트레이닝 데이터의 갯수






・n은 feature의 개수, m은 트레이닝 데이터의 개수

x[:10] ➡(100,3)matrix
array([
[ 2.48270246, 2.20781622, 1. ],
[ 6.07241833, 9.19025007, 1. ],
[ 3.11546929, 4.64238367, 1. ],
[10.81785453, 3.26464437, 1. ],
[12.07014858, 4.42723458, 1. ],
[11.83337984, 5.07817642, 1. ],
[13.12434071, 10.7762702 , 1. ],
[ 9.89781386, 15.71398351, 1. ],
[10.00780438, 16.26077027, 1. ],
[17.19363062, 12.50682637, 1. ]])
y[:10] ➡(100,)vector
array([533.83030493, 526.31007838, 532.42415066, 531.48943805, 533.43500502, 539.84331102, 535.17117282, 532.18836072, 541.13287791, 536.28514281])
# predictions is (100, )vector by dot product.


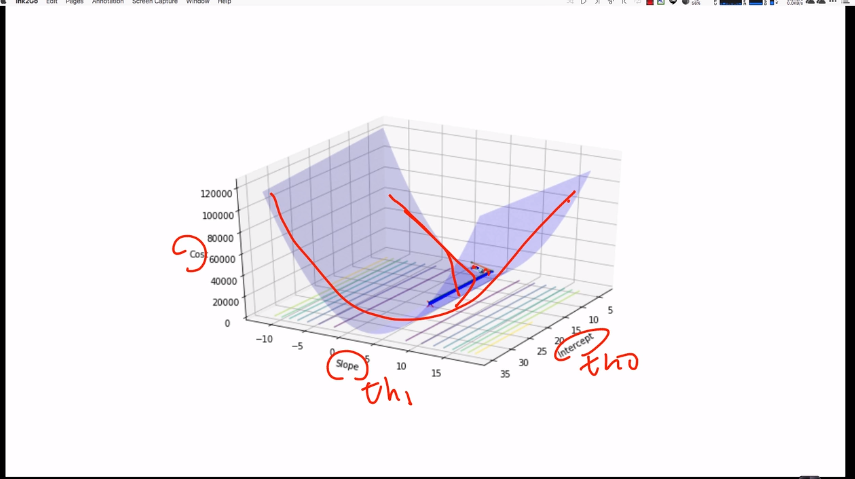
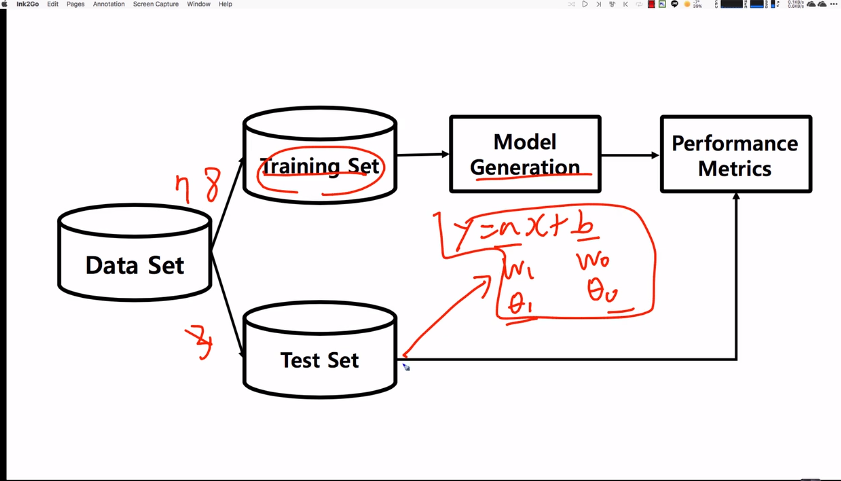
Multivariate linear regression models
assignment
import numpy as np
class LinearRegressionGD(object):
def __init__(self, fit_intercept=True, copy_X=True,
eta0=0.001, epochs=1000, weight_decay=0.9):
self.fit_intercept = fit_intercept
self.copy_X = copy_X
self._eta0 = eta0
self._epochs = epochs
self._cost_history = []
self._coef = None
self._intercept = None
self._new_X = None
self._w_history = []
self._weight_decay = weight_decay
######################
# %function$ [cost]
# %param$ [h] : numpy array, 2차원 matrix 형태로 [-1, n_predicted_targets]의 구조를 가진다.
# %param$ [y] : numpy array, 실제 y 값을 1차원 vector 형태로 [n_real_values]의 구조를 가진다.
# %return$ [cost_value] : cost_value : float형태의 scalar 값을 반환함
######################
def cost(self, h, y):
# y = y.reshape(-1,1)
# cost_value = (1/(2*len(y)))*(np.sum((h-y)**2))
# return cost_value
return (1/(2*len(y)))*(np.sum((h-y.reshape(-1,1))**2))
######################
# %function$ [hypothesis_function]
# %param$ [X] : numpy array, 2차원 matrix 형태로 [n_samples,n_features] 구조를 가진다
# %param$ [theta] : numpy array, 가중치 weight값을 1차원 vector로 입력한다.
# %return$ [Y_hat] : y_hat : numpy array, 예측된 값을 2차원 matrix 형태로 [-1, n_predicted_targets]의 구조를 가진다.
######################
def hypothesis_function(self, X, theta):
# y_hat = np.dot(X, theta)
# y_hat = y_hat.reshape(-1,1)
# return y_hat
return np.dot(X, theta).reshape(-1,1)
######################
# %function$ [cost]
# %param$ [X] : numpy array, 2차원 matrix 형태로 [n_samples,n_features] 구조를 가진다
# %param$ [y] : numpy array, 실제 y 값을 1차원 vector 형태로 [n_real_values]의 구조를 가진다.
# %param$ [theta] : numpy array, 가중치 weight값을 1차원 vector로 입력한다.
# %return$ [cost_value] : numpy array, 공식에 의해 산출된 gradient vector를 반환함.
# 이때 gradient vector는 weight의 갯수 만큼 element를 가진다.
# 반환되는 형태는 자유롭게 할 수 있으나 [-1, weight_gradient]나
# weight_gradient]로 반환 후 다음 수식에서 사용하기 위한 처리가 필요하다.
# 현재는 벡터를 반환함
######################
def gradient(self, X, y, theta):
m = len(y)
alpha = self._eta0
y_prediction = np.dot(X,theta)
for i in range(theta.size):
theta[i] = theta[i] - (alpha/m) * np.sum((y_prediction - y) * X[:,i])
# print(theta)
return theta
######################
# %function$ [fit]
# %param$ [X] : numpy array, 2차원 matrix 형태로 [n_samples,n_features] 구조를 가진다
# %param$ [y] : numpy array, 실제 y 값을 1차원 vector 형태로 [n_real_values]의 구조를 가진다.
# %return$ [self]
######################
def fit(self, X, y):
# Write your code
# if fit_intercept is true, create 1 as vector
if(self.fit_intercept):
x_rows = X.shape[0]
one_vector = np.ones(shape=(x_rows,1))
X = np.hstack((one_vector, X))
# save X to self._new_X
self._new_X = X
# initiate theta
theta = np.ones(X.shape[1])
# 1번의 full-batch가 데이터 전량을 사용하므로, 1epoch이라 할 수 있다.
# 여기선 epoch을 iteration이라고 생각하면 편하다.
for epoch in range(self._epochs):
# 아래 코드를 반드시 활용할 것
gradient = self.gradient(self._new_X, y, theta).flatten()
# cotrol learning rate
self._eta0 = self._eta0 * self._weight_decay
# Write your code
if epoch % 100 == 0:
self._w_history.append(theta)
cost = self.cost(self.hypothesis_function(self._new_X, theta), y)
self._cost_history.append(cost)
# Write your code
self._coef = theta[1:,]
self._intercept = theta[0]
# print('#####################theta[1:,]',theta[1:,])
# print('#####################theta[0]',theta[0])
# print(self._w_history)
return self
######################
# %function$ [hypothesis_function]
# %param$ [X] : numpy array, 2차원 matrix 형태로 [n_samples,n_features] 구조를 가진다
# %param$ [theta] : numpy array, 가중치 weight값을 1차원 vector로 입력한다.
# %return$ [Y_hat] : y_hat : numpy array, 예측된 값을 2차원 matrix 형태로 [-1, n_predicted_targets]의 구조를 가진다.
######################
def predict(self, X):
if(self.fit_intercept):
x_rows = X.shape[0]
one_vector = np.ones(shape=(x_rows,1))
X = np.hstack((one_vector, X))
theta = self._w_history[len(self._w_history)-1]
y = np.dot(X, theta)
return y
@property
def coef(self):
return self._coef
@property
def intercept(self):
return self._intercept
@property
def weights_history(self):
return np.array(self._w_history)
@property
def cost_history(self):
return self._cost_history









'C Lang > machine learing' 카테고리의 다른 글
| 확률적 경사하강법의 이해 (1) | 2019.04.15 |
|---|---|
| 8-1. Stochastic gradient descent(SGD)-linear regression, full-batch linear regression, stochastic gradient descent, mini-stochastic gradient descent (0) | 2019.04.15 |
| 7-5. Linear regression wtih gradient descent (0) | 2019.04.03 |
| 7-4. Gradient descent approach (0) | 2019.03.29 |
| 7-3. Normal equation (0) | 2019.03.26 |